Besaran vektor, besaran yang punya arah. Contoh: gaya (F), percepatan (a), kecepatan (v), momentum (p). sedangkan besaran skalar, besaran yang tak punya arah. Contoh: massa (m), panjang (L), waktu (t), kelajuan (v), massa jenis (ρ).
Vektor diberi nama dengan huruf kecil bergaris atas atau menyebut titik pangkal dan ujungnya.
1) Anak panah menunjuk arah yang ditunjuk vektor.
2) Besar kecilnya vektor dilambangkan dengan besar kecilnya anak panah.
Nilai arah vektor:
1) Vektor positif pada koordinat kartesius arahnya ke atas (terhadap y) atau ke kanan (terhadap x).
2) Vektor negatif pada koordinat kartesius arahnya ke bawah (terhadap y) atau ke kiri (terhadap x).
3) Vektor memiliki resultan yang merupakan hasil dari penjumlahan, pengurangan atau perkaliannya.
PENJUMLAHAN DAN PENGURANGAN VEKTOR
1. Penjumlahan dan Pengurangan vektor digunakan untuk mencari resultan vektor.
2. Resultan vektor dapat dicari dengan menghubungkan pangkal vektor awal dengan ujung vektor akhir.
- Cara Segitiga (dua vektor)

- Cara Jajar Genjang (dua vektor)
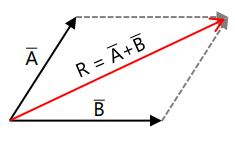
- Cara Poligon (lebih dari dua vektor)
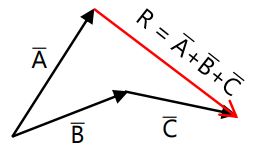
3. Pengurangan vektor dapat menggunakan sifat operasi hitung:
R = A̅ – B̅ = A̅ + (-B̅) (berbalik arah)
Contoh:
Jika diketahui arah vektor A, B, dan C sebagai berikut,
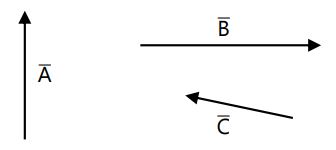
maka tentukan,
a. Resultan A̅ + B̅
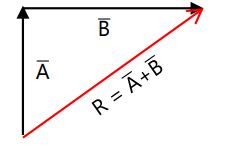
b. Resultan A̅ – B̅
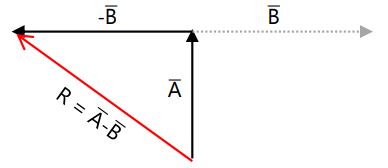
c. Resultan A̅ – C̅
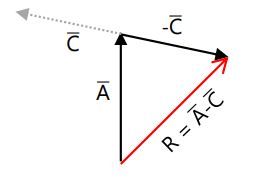
d. Resultan –(B̅ + C̅)

e. Resultan A̅ – B̅ – C̅ dan A̅ + B̅ + C̅
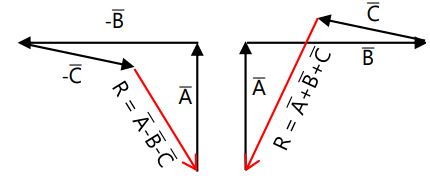
Adapun persamaan resultan vektor dapat dirumuskan:
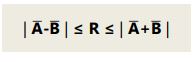
PENJUMLAHAN VEKTOR SECARA ANALITIK
Sebuah vektor dapat diuraikan menjadi dua buah vektor pada sumbu horizontal (x) dan sumbu vertikal (y). Vektor tersebut terurai menjadi komponen x dan y yang saling tegak lurus dan memiliki resultan dengan arah yang merupakan vektor yang terurai itu sendiri.
CARA MENENTUKAN KOMPONEN VEKTOR
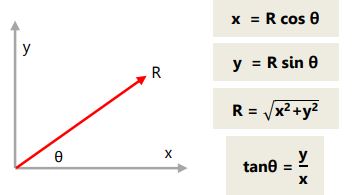
Adapun penjumlahan vektor secara analitik dapat dilakukan dalam tiga kondisi:
- Dua buah vektor yang tegak lurus
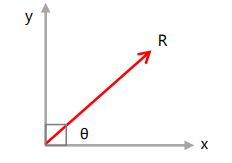
Resultan vektor dihitung menggunakan teorema Phytagoras:
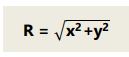
Sedangkan arah resultan terhadap sumbu x dapat dihitung:
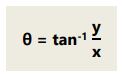
Contoh Soal:
Gaya 4 N yang bergerak ke arah utara dan gaya 10 N yang bergerak ke barat dilambangkan dengan vektor. Tentukan resultan dan arahnya! Jawabannya
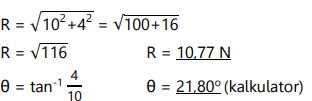
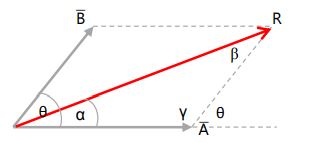
- Dua buah vektor yang tidak tegak lurus
Resultan vektor dihitung menggunakan persamaan kosinus:
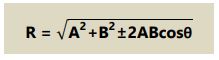
Sedangkan arah resultan terhadap sumbu x dapat dihitung dengan persamaan sinus:
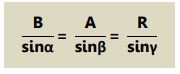
Contoh Soal:
Tentukan nilai resultan dan arah resultan vektor F1 dan F2!
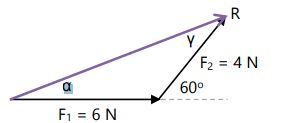
Jawab:

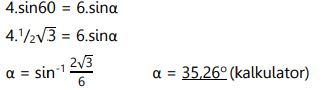
- Lebih dari dua buah vektor
Jika terdapat lebih dari dua buah vektor, harus diketahui terlebih dahulu resultan komponen x dan y nya, sehingga menjadi dua vektor yang tegak lurus, kemudian resultan baru dapat dicari.
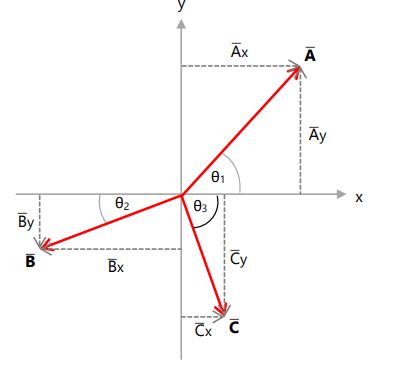
Resultan komponen vektor x:
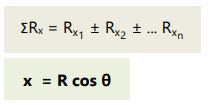
Resultan komponen vektor y:
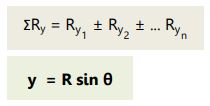
Setelah kedua komponen dihitung, maka susunan vektor menjadi:
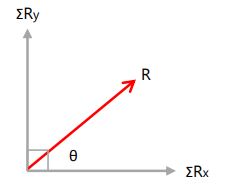
Resultan akhir vektor:
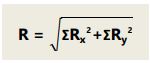
Arah resultan vektor:
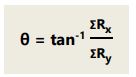
Contoh Soal:
Suatu benda ditarik oleh tiga buah gaya sesuai diagram dibawah. Tentukan resultan gaya dan arah perpindahan benda!
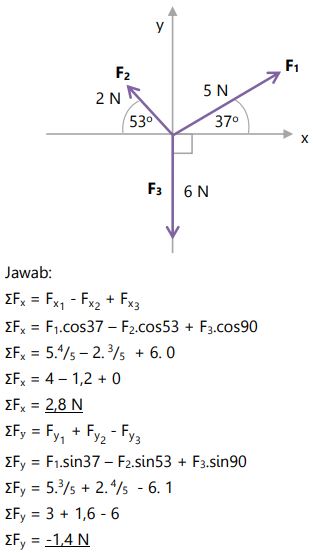
Kemudian dapat dibentuk menjadi

Maka dapat disimpulkan bahwa arah perpindahan adalah barat condong ke selatan sebesar 30 derajat.
Baca Juga Rangkuman Materi Angka Penting
PERKALIAN VEKTOR
Perkalian vektor terdiri dari dua, yaitu perkalian titik (dot), dan perkalian silang (cross).
BENTUK PENULISAN VEKTOR:
1. Vektor posisi, ditulis dalam notasi vektor terhadap titik acuan. Contoh: vektor posisi titik A dari O adalah OA̅.
2. Vektor basis, ditulis dalam vektor satuan.
Vektor satuan sumbu x adalah i, sumbu y adalah j, dan sumbu z adalah k.
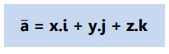
Panjang/nilai skalar dari vektor yang ditulis dalam vektor basis adalah:
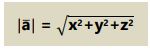
3. Perkalian skalar/titik (•) menghasilkan besaran skalar, memiliki definisi:
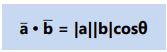
4. Perkalian skalar dengan vektor basis dengan a̅ = (x1, y1, z1) dan b̅ = (x2, y2, z2) diketahui dapat dihitung:
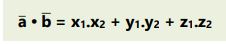
SIFAT-SIFAT PERKALIAN SKALAR:

PERKALIAN VEKTOR/SILANG (X) menghasilkan besaran vektor yang tegak lurus terhadap dua vektor yang dikali silang, memiliki definisi:
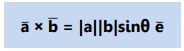
Perkalian vektor dengan vektor basis dengan a̅ = (x1, y1, z1) dan b̅ = (x2, y2, z2) diketahui dapat dihitung:
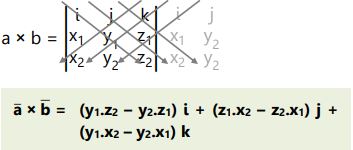
SIFAT-SIFAT PERKALIAN VEKTOR:

Sudut dua vektor dapat dicari menggunakan perkalian skalar.



Leave a Reply
You must be logged in to post a comment.